| Predicted | Positive | Negative |
|---|---|---|
| Positive | A - TP | B-FP |
| Negative | C - FN | D-TN |
Measuring Performance
Dr. Thiyanga S. Talagala
Department of Statistics, Faculty of Applied Sciences
University of Sri Jayewardenepura, Sri Lanka
Department of Statistics, Faculty of Applied Sciences
University of Sri Jayewardenepura, Sri Lanka
Measures for Regression
Loss function
- Function that calculates loss for a single data point
\(e_i = y_i - \hat{y_i}\)
\(e_i^2 = (y_i - \hat{y_i})^2\)
Cost function
- Calculates loss for the entire data sets
\[ME = \frac{1}{n}\sum_{i=1}^n e_i\]
Numeric outcome: Evaluations
Prediction accuracy measures (cost functions)
Mean Error
\[ME = \frac{1}{n}\sum_{i=1}^n e_i\]
- Error can be both negative and positive. So they can cancel each other during the summation.
Mean Absolute Error (L1 loss)
\[MAE = \frac{1}{n}\sum_{i=1}^n |e_i|\]
Mean Squared Error (L2 loss)
\[MSE = \frac{1}{n}\sum_{i=1}^n e^2_i\]
Mean Percentage Error
\[MPE = \frac{1}{n}\sum_{i=1}^n \frac{e_i}{y_i}\]
Mean Absolute Percentage Error
\[MAPE = \frac{1}{n}\sum_{i=1}^n |\frac{e_i}{y_i}|\]
Root Mean Squared Error
\[RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^n e^2_i}\]
Visualizaion of error distribution
Graphical representations reveal more than metrics alone.
Accuracy Measures on Training Set vs Test Set
Accuracy measure on training set: Tells about the model fit
Accuracy measure on test set: Model ability to predict new data
Evaluate Classifier Against Benchmark
Naive approach: approach relies soley on \(Y\)
Outcome: Numeric
Naive Benchmark: Average (\(\bar{Y}\))
A good prediction model should outperform the benchmark criterion in terms of predictive accuracy.
Measures for predicted classes
Confusion matrix/ Classification matrix
TP - True Positive
FP - False Positive
FN - False Negative
TN - True Negative
\(A\) - True Positive
\(B\) - False Positive
\(C\) - False Negative
\(D\) - True Negative
\[Sensitivity = \frac{A}{A+C}\]
\[Specificity = \frac{D}{B+D}\]
\[Prevalence = \frac{A+C}{A+B+C+D}\]
\[\text{Detection Rate} = \frac{A}{A+B+C+D}\]
\[\text{Detection Prevalence} = \frac{A+B}{A+B+C+D}\]
\[\text{Balance Accuracy}=\frac{Sensitivity + Specificity}{2}\]
\[Precision = \frac{A}{A+B}\]
\[Recall = \frac{A}{A+C}\]
F-1 score
\[F_1 = \frac{2 \times (\text{precision} \times \text{recall})}{\text{precision + recall}}\] The \(F1\) score can be interpreted as a harmonic mean of the precision and recall, where an \(F1\) score reaches its best value at 1 and worst score at 0. The relative contribution of precision and recall to the F1 score are equal.
F-beta score
\[F_1 = \frac{(1+\beta^2) \times (\text{precision} \times \text{recall})}{(\beta^2 \times \text{precision}) + \text{recall}}\]
Weighted harmonic mean of the precision and recall, reaching its optimal value at 1 and worst value at 0.
The beta parameter determines the weight of recall in the combined score.
\[\beta < 1 - \text{more weight to precision }\]
\[\beta > 1 - \text{favors recall}\]
Positive Prediction Value (PPV)
\[PPV = \frac{sensitivity \times prevalence}{(sensitivity \times prevalence)+((1-specificity)\times (1-prevalence))}\]
Negative Prediction Value (PPV)
\[NPV = \frac{specificity \times (1-prevalence)}{( (1-sensitivity) \times prevalence)+(specificity \times (1-prevalence))}\]
Receiver Operating Characteristic (ROC) curve
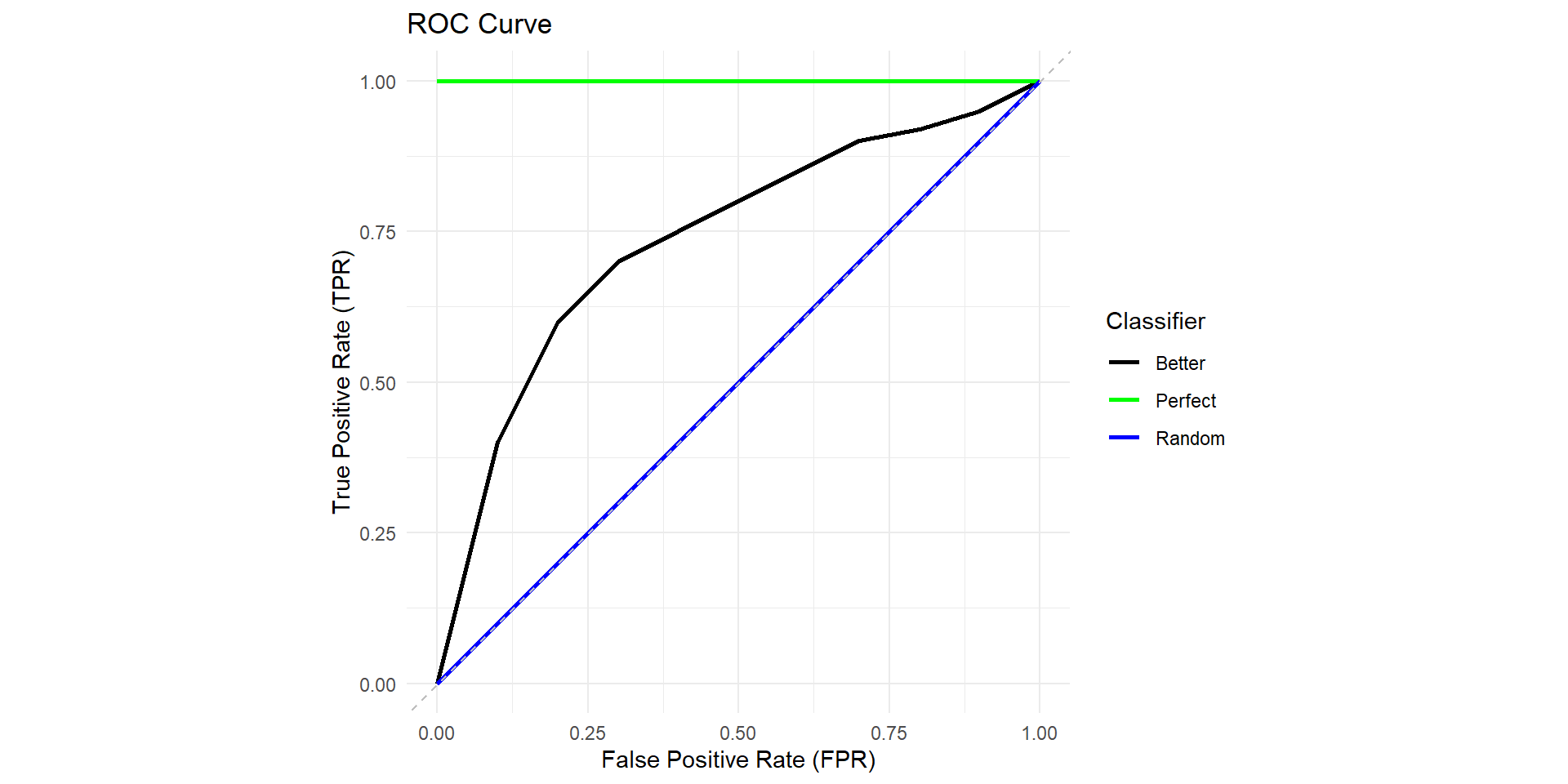
\[TPR = \frac{TP}{TP+FN}\]
\[FPR = \frac{FP}{FP+TN}\]
Area Under Curve (AUC)
Perfect classifier: \(AUC = 1\)
Random classifier: \(AUC = 0.5\)