5 Applications
5.1 Computer Science
5.1.1 PageRank Algorithm
Eirinaki, M., Vazirgiannis, M., & Kapogiannis, D. (2005, November). Web path recommendations based on page ranking and markov models. In Proceedings of the 7th annual ACM international workshop on Web information and data management (pp. 2-9).
Extracted “Markov models have been widely used for modelling users’ navigational behaviour in the Web graph, using the transitional probabilities between web pages, as recorded in the web logs. The recorded users’ navigation is used to extract popular web paths and predict current users’ next steps. Such purely usage-based probabilistic models, however, present certain shortcomings. Since the prediction of users’ navigational behaviour is based solely on the usage data, structural properties of the Web graph are ignored.”
5.1.2 Machine Learning
- Hidden Markov Models (HMMs) are widely used in speech recognition and natural language processing.
5.1.3 Monte Carlo Markov Chain (MCMC) Applications
Randomized Algorithms – Monte Carlo Markov Chain (MCMC) methods are used in simulations and Bayesian inference.
Markov Chain Monte Carlo (MCMC) is a class of algorithms used to sample from complex probability distributions when direct sampling is difficult. It combines Markov chains with Monte Carlo methods to generate samples that approximate a target distribution.
How MCMC Works
Markov Chain Property
The process moves from one state to another based on a transition rule, where the next state depends only on the current state (not past states).
Monte Carlo Sampling
Random samples are generated to approximate integrals, expectations, or probabilities in Bayesian inference and statistical modeling.
Convergence to Target Distribution
Over many iterations, the chain reaches a steady-state (stationary distribution) that represents the desired probability distribution.
Popular MCMC Algorithms
Metropolis-Hastings Algorithm
Gibbs Sampling
Hamiltonian Monte Carlo (HMC)
Applications of MCMC
Bayesian Statistics → Posterior inference in Bayesian models.
Machine Learning → Parameter estimation in probabilistic models.
Physics & Chemistry → Simulating molecular dynamics and statistical mechanics.
Finance → Risk assessment and portfolio optimization.
Genetics & Epidemiology → Evolutionary models and disease spread prediction
5.2 Biology
5.2.1 Population Genetics – Evolutionary changes in gene frequencies are modeled with Markov chains.
5.2.2 Ecological Modelling
Balzter, H. (2000). Markov chain models for vegetation dynamics. Ecological modelling, 126(2-3), 139-154.
Extracted “The aim of this paper is to assess the applicability of Markov chain models to predict vegetation changes using several different data sets, both from the scientific literature and own observations. It is anticipated that the results and the insights in model behaviour will also be useful for large-scale landscape ecosystem models by using Markov chains as submodels.”
5.2.3 Epidemiology – Predicting disease spread using Markov models in SIR models.
Teaching in the Time of the COVID-19 Pandemic: dynamic Markov models in epidemiology
Susceptible Infected Recovered (SIR)
Susceptible Exposed Infected Recovered (SEIR)
5.2.3.1 Dynamic Markov Models (DMMs)
DMMs refer to Markov models where transition probabilities change over time, making them more flexible than standard homogeneous Markov chains. These models are useful in scenarios where the system evolves dynamically, such as in financial markets, weather forecasting, and biological processes.
Another application of DMM
Guo, X., Liu, Y., Tan, K., Mao, W., Jin, M., & Lu, H. (2021). Dynamic Markov Model: Password Guessing Using Probability Adjustment Method. Applied Sciences, 11(10), 4607. https://doi.org/10.3390/app11104607
Extracted
“Password attack technology is mainly used for recovering passwords…”
5.2.3.2 Susceptible-Infected-Recovered (SIR) models
These model assumes people can be in 3 states:
1 Susceptible: people have no immunity to the disease. These people can become infected by coming into contact with an infected person.
2 Infected: people have the disease and they can spread it.
3 Recovered people survive the disease and have immunity.
These are states as we saw before but in these models they are referred as compartments. For this reason models like these are called compartmental disease models. However, there is not much agreement on names, but you can think of these models as dynamic Markov models that come in two flavors, deterministic and stochastic.
They are “dynamic” because people move from one compartment (state) to the other at different rates over time. In other words, the transition probabilities are not fixed, they change over time.
The transition probabilities are themselves a function of other parameters in the model (which we will cover soon).
The SIR model description is extracted from here.
5.3 Economics
5.3.1 Consumer Behavior Modeling – Predicting how consumers switch between different brands.
- Sharma, V., & Sonwalkar, J. (2016). Predicting the Switching Intention of Cell-Phone Brands: Application of Markov Chain Models. Journal of Management Research and Analysis, 3(2), 95-100.
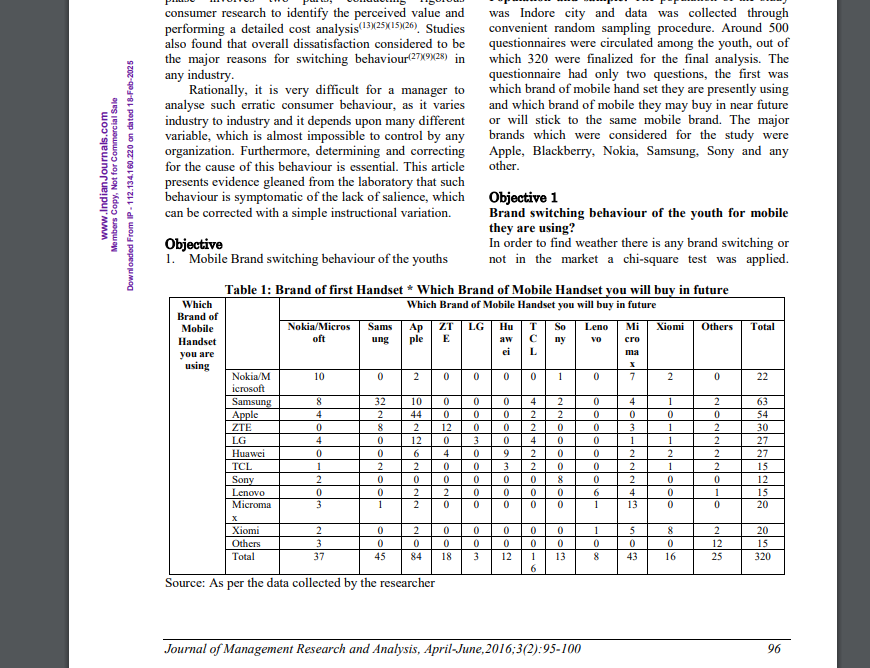
The above image is extracted from the paper “Sharma, V., & Sonwalkar, J. (2016). Predicting the Switching Intention of Cell-Phone Brands: Application of Markov Chain Models. Journal of Management Research and Analysis, 3(2), 95-100.”