3  Built-in-Functions in R

3.1 Built-in-Functions

Built-in functions are predefined functions that come with R (or any programming language). You don’t need to define them yourself. They are available to use immediately after starting R.

3.1.1 How Built-in Functions Work

A function call in R is always written as:

function_name(arguments)

Parentheses () are always required.

Inside the parentheses, you place the inputs (arguments) that the function needs to work.

Example

mean(1:10)
[1] 5.5

To obtain the help file of a function you can type

?mean

or

help(mean)

3.2 Commonly used mathematical functions

3.2.1 Basic Arithmetic Functions

sum(1, 2, 3, 4)        # Sum → 10
[1] 10
prod(2, 3, 4)          # Product → 24
[1] 24
abs(-7)                # Absolute value → 7
[1] 7
sign(-15)              # Sign → -1
[1] -1
sqrt(25)               # Square root → 5
[1] 5
factorial(5)           # Factorial → 120
[1] 120
cumsum(c(1,2,3,4))     # Cumulative sum → 1 3 6 10
[1]  1  3  6 10
cumprod(c(1,2,3,4))    # Cumulative product → 1 2 6 24
[1]  1  2  6 24

3.2.2 Exponentials and Logarithms

exp(1)                 # e^1 → 2.718282
[1] 2.718282
log(10)                # Natural log → 2.302585
[1] 2.302585
log10(1000)            # Base-10 log → 3
[1] 3
log2(8)                # Base-2 log → 3
[1] 3

3.2.3 Rounding and Approximations

round(3.14159, 2)      # Round to 2 decimal places → 3.14
[1] 3.14
ceiling(3.2)           # Round up → 4
[1] 4
floor(3.8)             # Round down → 3
[1] 3
trunc(3.9)             # Remove decimal → 3
[1] 3
signif(3.14159, 3)     # Significant digits → 3.14
[1] 3.14

3.2.4 Trigonometric Functions

sin(pi/2)              # Sine → 1
[1] 1
cos(0)                 # Cosine → 1
[1] 1
tan(pi/4)              # Tangent → 1
[1] 1
asin(1)                # Inverse sine → π/2
[1] 1.570796
acos(0)                # Inverse cosine → π/2
[1] 1.570796
atan(1)                # Inverse tangent → π/4
[1] 0.7853982

3.2.5 Hyperbolic Functions

sinh(1)                # Hyperbolic sine
[1] 1.175201
cosh(1)                # Hyperbolic cosine
[1] 1.543081
tanh(1)                # Hyperbolic tangent
[1] 0.7615942

3.2.6 Miscellaneous

max(1,4,2,5)           # Maximum → 5
[1] 5
min(1,4,2,5)           # Minimum → 1
[1] 1
range(1,4,2,5)         # Range → 1 5
[1] 1 5

3.3 Commonly used statistics functions

Sample data

x <- c(5, 7, 9, 10, 12, 15, 18)
y <- c(2, 4, 6, 8, 10, 12, 14)

3.3.1 Measures of Central Tendency

mean(x) # mean
[1] 10.85714
median(x) # median
[1] 10

3.3.2 Measures of Spread

var(x) # variance
[1] 20.47619
sd(x) # standard deviation
[1] 4.525062
range(x) # range
[1]  5 18
IQR(x) # Inter Quartile Range
[1] 5.5

3.3.3 Percentiles / Quantiles

quantile(x, probs = c(0.25, 0.5, 0.75)) # quantiles
 25%  50%  75% 
 8.0 10.0 13.5 
quantile(x, probs = 0.9) # percentiles
 90% 
16.2

3.3.4 Correlation and Covariance

cov(x, y) # Covariance
[1] 19.33333
cor(x, y) # correlation
[1] 0.9888918

3.4 Probability distribution functions

  • Each probability distribution in R is associated with four functions.

  • Naming convention for the four functions:

    For each function there is a root name. For example, the root name for the normal distribution is norm. This root is prefixed by one of the letters d, p, q, r.

    • d prefix for the distribution function

    • p prefix for the cumulative probability

    • q prefix for the quantile

    • r prefix for the random number generator

  • Example: dnorm, pnorm, qnorm, rnorm

3.4.1 Illustration with Standard normal distribution

The general formula for the probability density function of the normal distribution with mean \(\mu\) and variance \(\sigma\) is given by

\[ f_X(x) = \frac{1}{\sigma\sqrt{(2\pi)}} e^{-(x-\mu)^2/2\sigma^2} \]

If we let the mean \(\mu=0\) and the standard deviation \(\sigma=1\), we get the probability density function for the standard normal distribution.

\[ f_X(x) = \frac{1}{\sqrt{(2\pi)}} e^{-(x)^2/2} \]

\[ f_X(x) = \frac{1}{\sqrt{(2\pi)}} e^{-(x)^2/2} \]

3.4.2 dnorm

dnorm(0)
[1] 0.3989423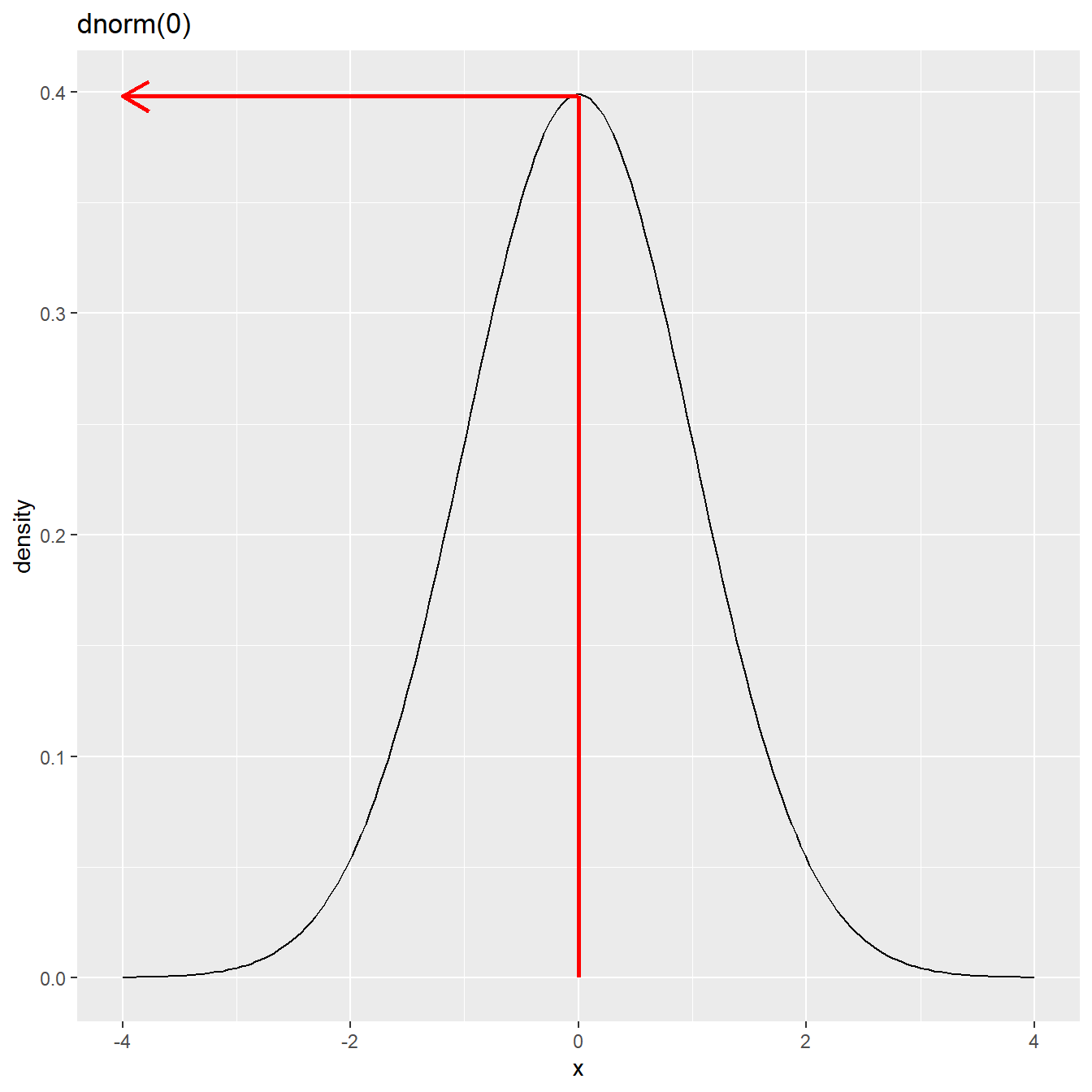

Standard normal probability density function: dnorm(0)

3.4.3 pnorm

pnorm(0)
[1] 0.5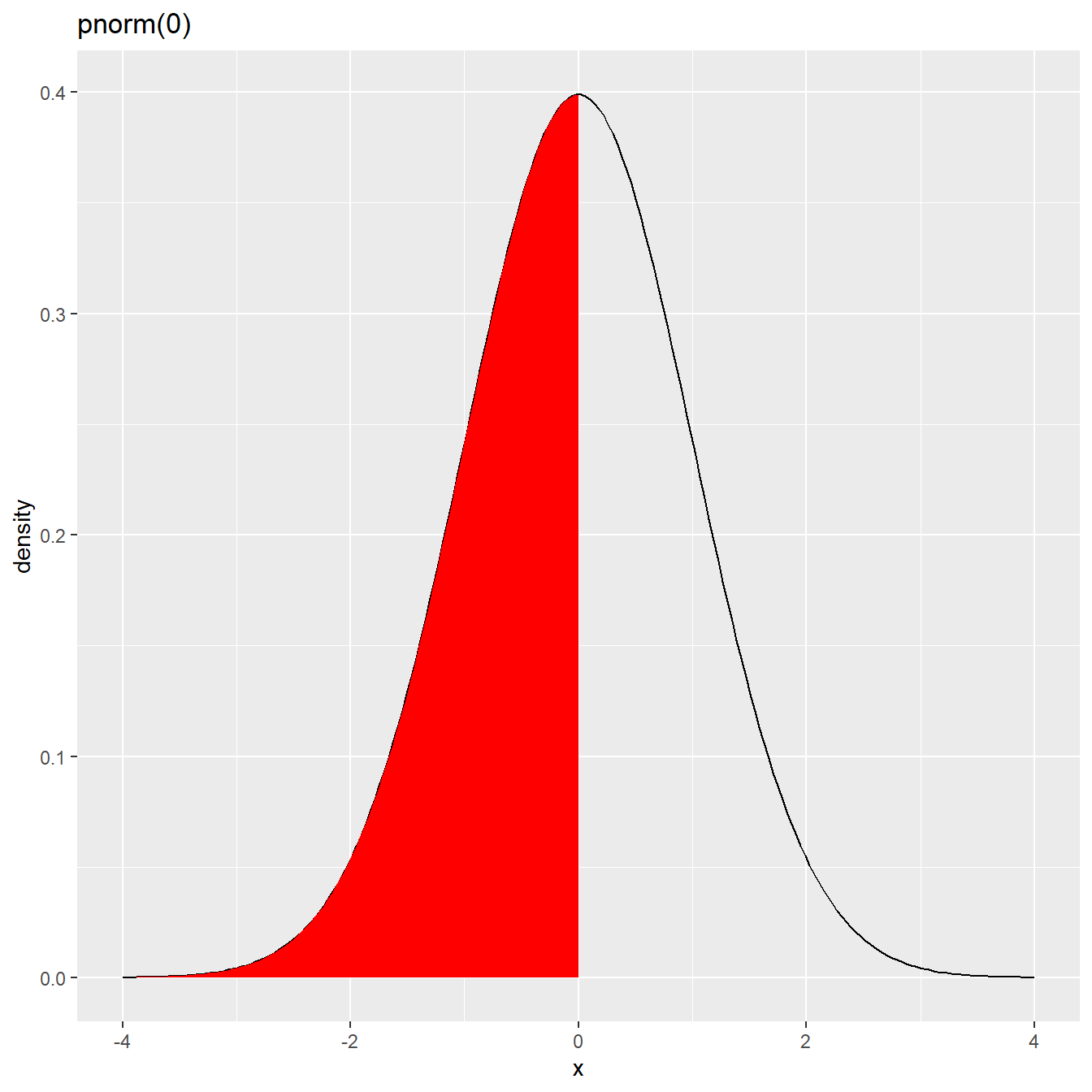

Standard normal probability density function: pnorm(0)

]

3.4.4 qnorm

qnorm(0.5)
[1] 0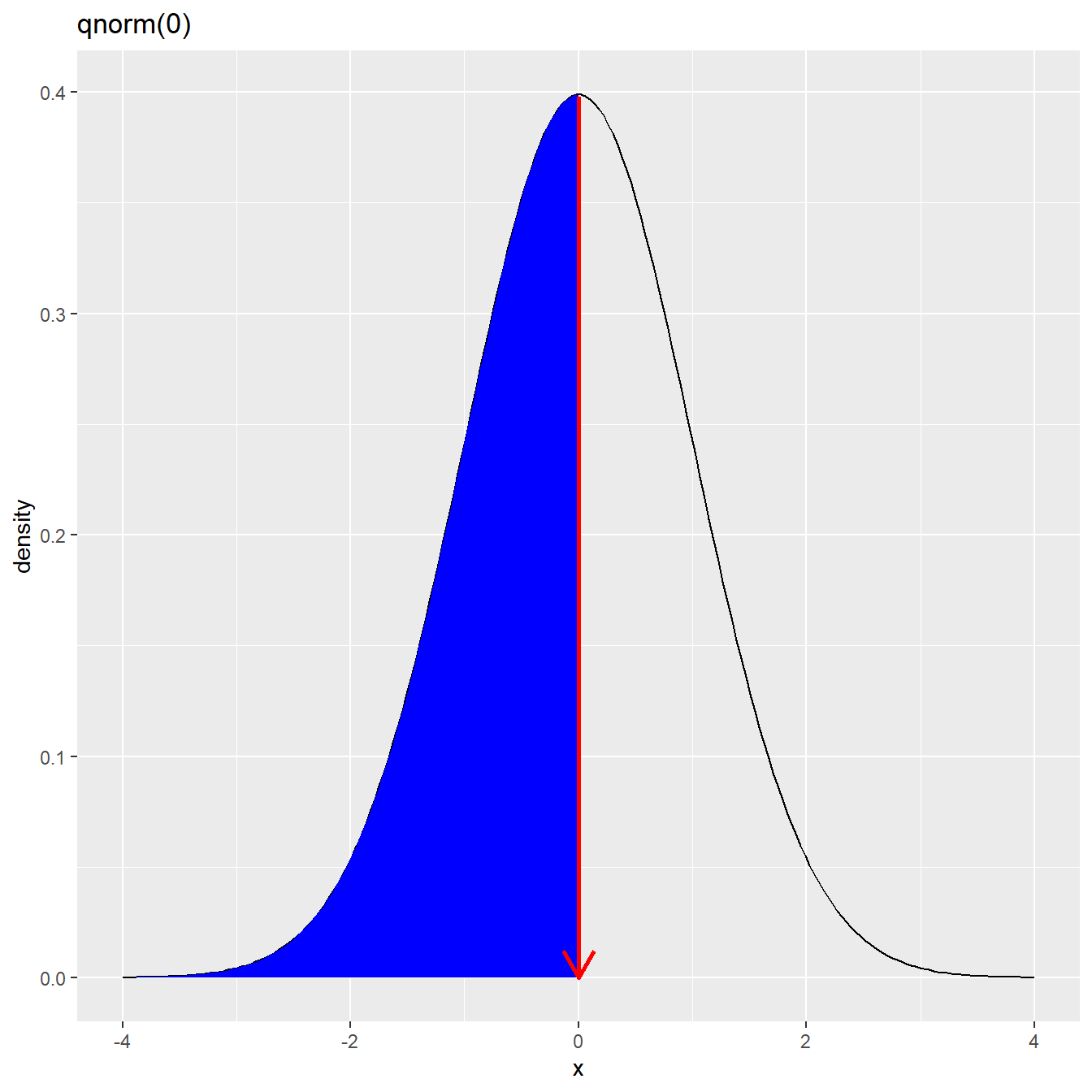

Standard normal probability density function: qnorm(0.5)

3.5 Test and Type conversion functions

Test Convert
is.numeric() as.numeric()
is.character() as.character()
is.vector() as.vector()
is.matrix() as.matrix()
is.data.frame() as.data.frame()
is.factor() as.factor()
is.logical() as.logical()
is.na()